Per què els índexs de refracció òptics són tan petits?
Un equip de científics descriu una nova teoria que pot explicar per què l’índex de refracció d’un medi atòmic desordenat només pot arribar a un valor màxim.
La portada de l’àlbum “Dark Side of the Moon” de Pink Floyd, votat com el millor àlbum de rock clàssic de tots els temps, retratava un prisma dispersant la llum en un arc de Sant Martí amb un cert simbolisme metafòric. El que el grup mai es va imaginar és que aquesta imatge es faria servir per ajudar a il·lustrar el concepte d’índex de refracció de la llum, i com aquesta canvia de velocitat i de direcció quan es troba amb un mitjà diferent al buit.
Encara que conceptualment el dibuix no sigui exacte, transmet el missatge que la llum canvia de velocitat al moure’s per un altre mitjà, i que les velocitats, diferents segons cada color, fan que la llum blanca es dispersi en els seus components. Aquest canvi de velocitat està relacionat amb l’índex de refracció, un nombre sense unitats que representa la relació entre la velocitat de la llum en el buit i la velocitat de la llum en un mitjà.
En general, tots els materials amb índexs de refracció positius tenen valors propers a 1 per a la llum visible. Però mai s’ha determinat del tot si això es deu únicament a una coincidència o reflecteix conceptes físics més complexos.
Investigant el valor màxim de l’índex
En un estudi publicat recentment a la revista Physical Review X i destacat pels editors, els investigadors de l’ICFO Francesco Andreoli i el professor ICREA a l’ICFO Darrick Chang, part del projecte en simulació quàntica QUASI-CAT, descriuen en col·laboració amb investigadors de la Universitat de Princeton, la Universitat de Chicago i l’Institut d’ ‘Optique, per què l’índex de refracció d’un gas atòmic diluït té un valor màxim de 1,7 independentment de la valor de la densitat dels àtoms.
Aquest resultat contrasta amb les teories convencionals dels llibres de text, que prediuen que com més material hi ha, major pot ser la resposta òptica i l’índex de refracció. Per poder abordar correctament els motius pels quals això ocorre, s’han de tenir en compte tant la multiplicitat de la dispersió de la llum – tots els possibles camins que pot seguir la llum al travessar un mitjà – i la interferència resultant. Aquest fenomen provoca que cada àtom individual vegi una intensitat de llum local, molt diferent de la intensitat enviada, i que variï en funció de la geometria dels àtoms que l’envolten. En lloc de tractar amb els complexos detalls microscòpics d’aquesta granularitat, fins ara els llibres de text sovint han assumit d’alguna manera que aquesta granularitat i els seus efectes sobre la llum poden suavitzar-se o fer-se més homogenis.
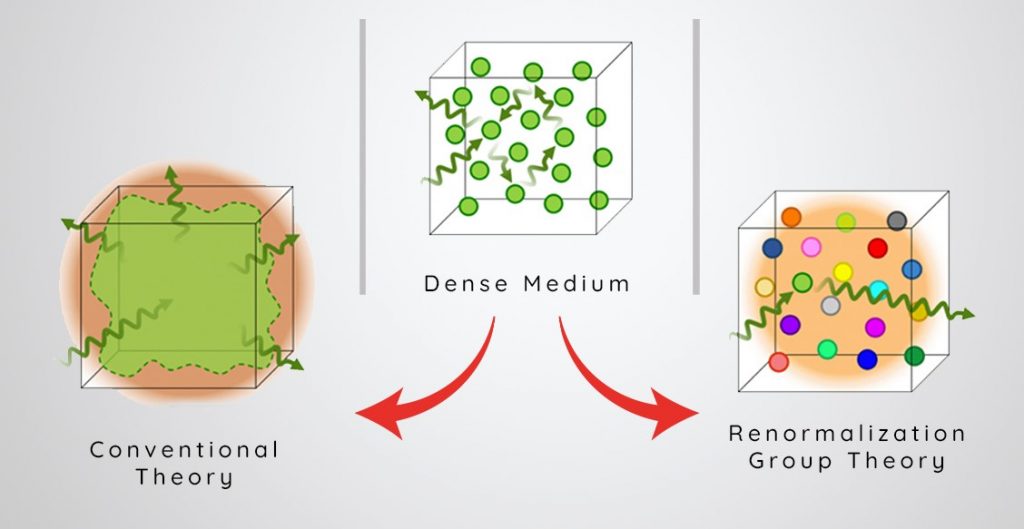
Una nova teoria: La re-normalització del desordre fort
Per contra, l’equip present una nova teoria, que han anomenat teoria de la re-normalització del desordre fort (RG), que els permet capturar la granularitat i els efectes de la dispersió múltiple d’una manera simple. Aquesta teoria descriu com la resposta òptica de qualsevol àtom es veu desproporcionadament afectada pel seu àtom veí més proper, a causa de les interaccions de camp proper, raó per la qual fallen les teories típiques d’homogeneïtat. L’efecte físic de les interaccions de camp proper és produir un eixamplament, no homogeni, de les freqüències de ressonància atòmica, on la quantitat d’eixamplament creix a mesura que creix la densitat. Això vol dir que no importa com d’alta sigui la densitat física dels àtoms; la llum entrant de qualsevol freqüència només veurà aproximadament 1 àtom quasi-ressonant per longitud d’ona cúbica per dispersar de manera eficient, fet que limitarà l’índex de refracció al seu valor màxim d’1,7.
En termes més generals, aquest estudi suggereix que la teoria RG podria constituir una nova eina per comprendre el problema de la dispersió múltiple de la llum, en mitjans desordenats cuasi-ressonants. Entre aquests mitjans s’inclouen també els règims no lineals i els règims quàntics. A més a més, la teoria obre la porta a estudiar els límits de l’índex de refracció en materials reals, començant pels àtoms individuals que els componen.
Més informació
Article citat: F. Andreoli, M. Gullans, A. A. High, A. Browaeys, and D. Chang. 2021. Maximum Refractive Index of an Atomic Medium. Phys. Rev. X 11, 011026.
Notícia destacada a APS Physics: https://link.aps.org/doi/10.1103/Physics.14.s12